Naucz się szybko i łatwo chemii fizycznej z kursem skrojonym pod studentów

Układ i otoczenie, ciepło i praca (formy energii), energia wewnętrzna, funkcje stanu

Praca objętościowa – wzór na pracę, definicja, praca w rozprężaniu swobodnym, pod stałym ciśnieniem, w przemianie odwracalnej, równania stanu gazu (doskonałego, sztywnych kul, van der Waalsa)

Energia wewnętrzna, pochodna cząstkowa, zależność energii wewnętrznej od temperatury – molowa pojemność cieplna w stałej objętości, zależność energii wewnętrznej od objętości, ciepło

Entalpia, zależność entalpii od temperatury – molowa pojemność cieplna pod stałym ciśnieniem, zależność entalpii od ciśnienia, praca nieobjętościowa (techniczna), zależność molowej pojemności cieplnej pod stałym ciśnieniem i molowej pojemności cieplnej w stałej objętości

Energia wewnętrzna i entalpia jako funkcje stanu, prawo Hessa, ciepło reakcji biegnącej w przeciwnym kierunku, standardowa entalpia reakcji, standardowe ciepło tworzenia związku, standardowe ciepło spalania związku, określanie ciepła reakcji, ciepło tworzenia substancji w formie pierwiastkowej, ciepło reakcji w innej temperaturze

Funkcje stanu – wartości intensywne i ekstensywne, izobary, izotermy, izochory, zasada ekwipartycji energii, adiabata Poissona

Procesy samorzutne i niesamorzutne, procesy odwracalne i nieodwracalne, entropia, izotermiczne rozprężanie/sprężanie, zwiększenie temperatury, zmiana entropii w przemianach fazowych

Entropia przemian fazowych – reguła Troutona, dwa wzory na entropię, teoremat cieplny Nernsta, entropia w dowolnej temperaturze, entropia reakcji chemicznych, samorzutność procesów, nierówność Clausiusa, entropia procesu odwracalnego i nieodwracalnego, produkcja i transport entropii

Energia Helmholtza – energia swobodna, energia Gibbsa – entalpia swobodna, maksymalna praca objętościowa, maksymalna praca nieobjętościowa, zależność entalpii swobodnej od ciśnienia i temperatury, potencjał chemiczny, powinowactwo chemiczne – kryterium samorzutności reakcji

Stałe równowagi chemicznej (Kx, Kp, Kc), prawo działania mas, zależności między stałymi równowagi, związek między energią Gibbsa a ciśnieniową stałą równowagi reakcji, izobara van’t Hoffa, lotność i współczynnik lotności 

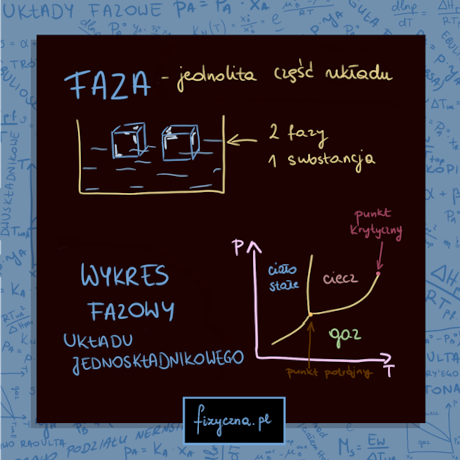Składniki i fazy w układzie, diagramy fazowe układów jednoskładnikowych, linie równowagi faz, punkt potrójny, punkt krytyczny – ciśnienie krytyczne i temperatura krytyczna, parowanie a wrzenie, normalna i standardowa temperatura wrzenia i topnienia, diagramy fazowe dla wysokich ciśnień, prawo Clausiusa-Clapeyrona, równania linii równowagi

Składniki niezależne w układzie, liczba stopni swobody, układy dwóch cieczy tworzących roztwory doskonałe, diagramy fazowe w układach dwóch cieczy tworzących roztwory doskonałe, dolna i górna krytyczna temperatura rozpuszczalności,

Prawo Raoulta, prawo Henry’ego, prawo Daltona, izobara rosy i izobara wrzenia

Destylacja frakcjonowana, azeotropy, układy ciecz – ciało stałe, zjawiska osmotyczne: ebuliometria i kriometria

Układy trójskładnikowe, trójkąt stężeń Gibbsa, prawo podziału Nernsta, konoda

Elektrochemia, elektrolity, dysocjacja elektrolityczna, stopień dysocjacji, standardowe entalpie i entalpie swobodne reakcji jonowych, współczynniki aktywności jonowej, średnie współczynniki aktywności

Graniczne prawo Debye’a-Huckla, iloczyn rozpuszczalności, równowagi kwasowo-zasadowe

Ogniwa elektrochemiczne (galwaniczne), elektrody, reakcje utleniania-redukcji, rodzaje ogniw, ogniwa w stanie równowagi

Równanie Nernsta dla ogniw w stanie równowagi, obliczanie stałej równowagi, standardowe napięcie ogniwa, potencjały standardowe półogniw, siła elektromotoryczna, konwencja Sztokholmska

Rodzaje ogniw

Wielkości termodynamiczne a napięcie ogniwa

Kinetyka chemiczna, szybkość i rząd reakcji, równania kinetyczne, stała szybkości reakcji i jej jednostka, reakcje elementarne

Reakcje zerowego, pierwszego, drugiego, trzeciego rzędu, reakcje n-tego rzędu, wyznaczanie rzędu reakcji

Zależność szybkości reakcji od temperatury, równanie Arrheniusa, czynnik częstości (przedwykładniczy), energia aktywacji

Reakcje złożone: reakcje odwracalne, reakcje następcze, reakcje łańcuchowe, reakcje równoległe

Kataliza, przybliżenie stanu stacjonarnego

W temperaturze 500°C i pod ciśnieniem 92.1 kPa gęstość par siarki wynosi 3.71 g∙dm-3 . Jaki jest wzór cząsteczkowy siarki w tych warunkach?

17g amoniaku o temperaturze 473 K zajmuje objętość 0.196 dm3. Obliczyć ciśnienie panujące w układzie traktując amoniak jako: a) gaz doskonały, b) gaz sztywnych kul, c) gaz van der Waalsa (a = 0.422 J∙m3∙mol-2, b = 51.4∙10-6 m3∙mol-1). Porównać wyniki.

Trzy mole gazu spełniającego równanie stanu sztywnych kul sprężono izotermicznie (398 K) w sposób odwracalny. Jaka jest wartość ciepła wymienionego z otoczeniem, jeśli ciśnienie gazu wzrosło dwukrotnie?

Obliczyć pracę, jaką wykonuje metan (2 mole CH4), gdy rozpręża się izotermicznie w temperaturze 300K objętości 1 dm3 do objętości 10 dm3, jeśli a) gaz przesuwa tłok obciążony stałym ciśnieniem 105 Pa, b) proces przebiega w sposób quasi statyczny.

Pewna ilość argonu zajmuje w 400 K i pod ciśnieniem 10^6 Pa objętość 1 dm3. Gaz ten rozpręża się adiabatycznie, przesuwając tłok obciążony ciśnieniem 105 Pa. Do jakiej objętości musi się rozprężyć, aby jego temperatura spadła do 390 K? Jak zmieni się energia wewnętrzna gazu?

Obliczyć końcową temperaturę 10 moli CO2 zajmujących pierwotnie, w 300 K, objętość 10−2 m3 po adiabatycznej ekspansji do zbiornika, z którego uprzednio wypompowano gaz do ciśnienia p = 0. Końcowa objętość gazu wynosiła 0.1 m3. Przyjąć, że CO2 spełnia równanie van der Waalsa i założyć, że pojemność cieplna Cv jest stała i wynosi 28.8 J·mol−1·K−1 (a dla CO2 wynosi 0.364 J·m3·mol−2).

Mol helu o temperaturze 300 K ogrzano pod stałym ciśnieniem p =10^5 Pa do temperatury 500 K, a następnie sprężono izotermicznie, quasi-statycznie do objętości jaką gaz zajmował na początku, po czym ochłodzono do 300 K bez zmiany objętości. Obliczyć pracę, ciepło, zmiany energii wewnętrznej i entalpii na każdym z etapów procesu. Hel traktować jak gaz doskonały.

Mol jednoatomowego gazu doskonałego znajdującego się pod ciśnieniem 10^6 Pa i objętości 2 dm3 rozpręża się izotermicznie w sposób odwracalny do ciśnienia 5·10^5 Pa (przemiana A) oraz rozpręża się adiabatycznie odwracalnie do ciśnienia 5·10^5 Pa (przemiana B). Dla obu przemian obliczyć wartości: Q, W, ∆U i ∆H. Przedstawić schematycznie na wykresie p = f(V) obydwie przemiany. Zaproponować przemianę przeprowadzającą gaz ze stanu końcowego przemiany B do stanu końcowego przemiany A.

Obliczyć zmianę entalpii 1 kg glinu w wyniku ogrzania go od 273 K do 1000 K. Glin topi się w 931.7 K, jego ciepło topnienia wynosi 10.7 kJ/mol, molową pojemność cieplną stałego glinu opisuje wyrażenie: Cp = 20.67+12.39·10−3T J/K·mol. Molowa pojemnośc ciekłego glinu w rozważanym przedziale temperatury jest w przybliżeniu stała i wynosi 29.25 J/K·mol.

1 mol wodoru poddano cyklowi przemian: (273 K, 22.4 dm3, pA) → (273 K, 11.2 dm3, pB) → (Tc, 50 dm3, pC =pB) → (500 K, 50 dm3 , pD ) → (TE, 22.4 dm3, pE, proces adiabatyczny). Wszystkie przemiany są odwracalne, wodór możemy traktować jak gaz doskonały, Cv = 2.5R, Cp = 3.5R. Obliczyć ∆U, ∆H, Q i W dla każdego etapu i dla całego procesu.

Standardowe molowe ciepła reakcji spalania butenu (C4H8), butanu (C4H10), węgla i wodoru wynoszą odpowiednio -2718,2 -2878,3 -393,51 i -285,84 kJ∙mol-1. Obliczyć standardowe molowe ciepła tworzenia: a) butenu, b) butanu oraz c) standardowe molowe ciepło uwodornienia butenu do butanu.

W butli znajduje się pod ciśnieniem nieznany gaz. Przypuszczamy, że jest to azot albo argon. Pobieramy próbkę gazu w temp. 25°C i rozprężamy adiabatycznie od 5 dm3 do 6 dm3. Temperatura podczas rozprężania spadła o 21 K. Który z gazów znajduje się w butli?

Opierając się na następujących danych obliczyć standardową molową entropię azotu w temp. 298 K. Ciepło molowe stałego azotu, Cp, w temperaturze 10 K wynosi 5.75 J·mol−1·K−1 , a przyrost entropii w przedziale 10 K – 35.61 K jest równy 20.25 J·mol−1K−1. W temperaturze 35.61 K następuje przejście w inną odmianę stałą, przy czym ciepło przemiany wynosi 228.9 J·mol−1 . Przyrost entropii od tej temperatury do temperatury topnienia (63.15 K) ma wartość 23.38 J·mol−1·K−1, a ciepło topnienia 720.9 J·mol−1. Przyrost entropii w przedziale temperatury od 63.14 do 77.32 (temperatura wrzenia) wynosi 11.41 J·mol−1·K−1, a ciepło parowania 5577 J·mol−1. Podczas ogrzewania gazu pod ciśnieniem 1 atm do temperatury 298 K jego entropa wzrasta o 39.20 J·mol−1·K−1.

 3 mole acetylenu poddano odwracalnej kompresji od V1 = 30 dm3 do V2 = 10dm3 w stałej temperaturze 320 K. Obliczyć wykonaną pracę, wymienione ciepło, ∆U, ∆H, ∆S, ∆G i ∆F zakładając, że acetylen stosuje się do równania gazu doskonałego.

Obliczyć Q, W, ∆U, ∆H, ∆S, ∆G i ∆F, gdy 1 mol gazu idealnego rozpręża się odwracalnie w temperaturze 298 K od V1 = 13.00 dm3 do V2 = 26.00 dm3. Jakie będą te wartości, jeżeli rozprężanie będzie przebiegać nieodwracalnie, przeciwko stałemu ciśnieniu równemu 0.5 bara?

Rurką z zaworem połączono dwa zbiorniki gazu. Obydwa były termostatowane w 25°C. Pierwszy zawierał 3 mole argonu pod ciśnieniem 4 barów, drugi mieścił 6 moli neonu pod ciśnieniem 2 barów. Po otwarciu zaworu oba gazy wymieszały się. Obliczyć ∆G i ∆S tego procesu przy założeniu, że gazy są doskonałe.

Mieszaninę zawierającą 45% HCl i 55% O2 ogrzano pod stałym ciśnieniem 723 mmHg do 753 K. Stan równowagi został osiągnięty gdy 76% HCl przereagowało zgodnie z reakcją: 4HCl(g) + O2(g) = 2Cl2(g) + 2H2O(g). Wyznacz Kp i Kc tej reakcji.

i wiele więcej.